1.
综合与探究
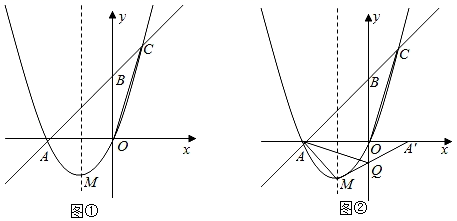
在平面直角坐标系中,抛物线y= x2+bx+c经过点A(﹣4,0),点M为抛物线的顶点,点B在y轴上,且OA=OB , 直线AB与抛物线在第一象限交于点C(2,6),如图①.
(1)
求抛物线的解析式;
(2)
直线AB的函数解析式为,点M的坐标为,cos∠ABO=;
(3)
在y轴上找一点Q , 使得△AMQ的周长最小.具体作法如图②,作点A关于y轴的对称点A',连接MA'交y轴于点Q , 连接AM、AQ , 此时△AMQ的周长最小.请求出点Q的坐标;
(4)
在坐标平面内是否存在点N , 使以点A、O、C、N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
连接OC , 若过点O的直线交线段AC于点P , 将△AOC的面积分成1:2的两部分,则点P的坐标为;
【考点】
待定系数法求二次函数解析式;
轴对称的应用-最短距离问题;
二次函数与一次函数的综合应用;
二次函数-动态几何问题;