1.
如图1,平面直角坐标系  中,等腰
中,等腰  的底边
的底边  在x轴上,
在x轴上,  ,顶点A在y的正半轴上,
,顶点A在y的正半轴上,  ,一动点
,一动点  从
从  出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿  向左运动,到达
向左运动,到达  的中点停止.另一动点F从点C出发,以相同的速度沿
的中点停止.另一动点F从点C出发,以相同的速度沿  向左运动,到达点O停止.已知点E、F同时出发,以
向左运动,到达点O停止.已知点E、F同时出发,以  为边作正方形
为边作正方形  ,使正方形
,使正方形  和
和  在
在  的同侧.设运动的时间为
的同侧.设运动的时间为  秒(
秒(  ).
).


(1)
当点H落在  边上时,求t的值;
(2)
设正方形
边上时,求t的值;
(2)
设正方形  与
与  重叠面积为S,请问是存在t值,使得
重叠面积为S,请问是存在t值,使得  ?若存在,求出t值;若不存在,请说明理由;
(3)
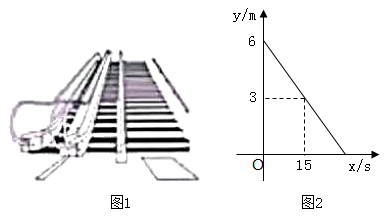
如图2,取
?若存在,求出t值;若不存在,请说明理由;
(3)
如图2,取  的中点D,连结
的中点D,连结  ,当点E、F开始运动时,点N从点O出发,以每秒
,当点E、F开始运动时,点N从点O出发,以每秒  个单位的速度沿
个单位的速度沿  运动,到达点O停止运动.请问在点E的整个运动过程中,点M可能在正方形
运动,到达点O停止运动.请问在点E的整个运动过程中,点M可能在正方形  内(含边界)吗?如果可能,求出点M在正方形
内(含边界)吗?如果可能,求出点M在正方形  内(含边界)的时长;若不可能,请说明理由.
内(含边界)的时长;若不可能,请说明理由.
【考点】
待定系数法求一次函数解析式;
等腰三角形的性质;
正方形的性质;
二次函数-动态几何问题;