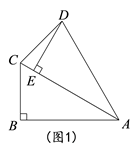1.
在一次数学研究性学习中, 小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1) ,其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动。
(1)
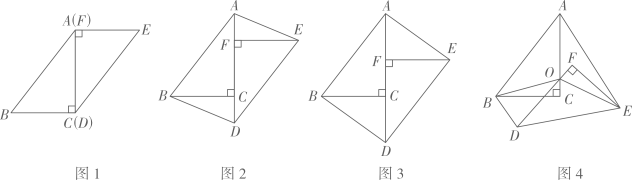
活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移。
(2)
活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4)。
【思考】图2中的四边形ABDE是平行四边形吗?请说明理由。
【发现】当纸片DEF平移到某一位置时,小兵发现四边形AB DE为矩形(如图3)。求AF的长。
【探究】当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由。
【考点】
全等三角形的判定与性质;
平行四边形的判定与性质;
旋转的性质;