1.
从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．
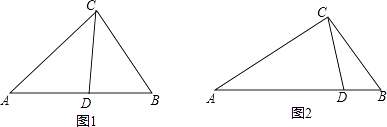
(1)
如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线．
(2)
在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数．
(3)
如图2，△ABC中，AC=2，BC= 
，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．
【考点】
相似三角形的判定与性质;
