如图，四棱柱ABCD﹣A1B1C1D1中，A1A⊥底面ABCD，四边形ABCD为梯形，AD∥BC，且AD=2BC，过A1、C、D三点的平面记为α，BB1与α的交点为Q．

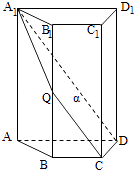
1. 如图，四棱柱ABCD﹣A₁B₁C₁D₁中，A₁A⊥底面ABCD，四边形ABCD为梯形，AD∥BC，且AD=2BC，过A₁、C、D三点的平面记为α，BB₁与α的交点为Q．

(1) 证明：Q为BB₁的中点；

(2) 求此四棱柱被平面α所分成上下两部分的体积之比；

(3) 若AA₁=4，CD=2，梯形ABCD的面积为6，求平面α与底面ABCD所成二面角的大小．

【考点】

棱柱、棱锥、棱台的体积; 用空间向量研究二面角; 二面角及二面角的平面角;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 如图，在圆台 $\text{[math]}$ 中，圆 $\text{[math]}$ 的半径是1，圆 $\text{[math]}$ 的半径是2，高是 $\text{[math]}$ ，圆 $\text{[math]}$ 是 $\text{[math]}$ 的外接圆， $\text{[math]}$ ， PC是圆台的一条母线．

(1) 求三棱锥 $\text{[math]}$ 体积的最大值；

(2) 当 $\text{[math]}$ 时，求平面PAC与平面PBC的锐二面角的余弦值．

解答题普通

2. 如图，在四棱锥 $\text{[math]}$ 中，侧面 $\text{[math]}$ 底面 $\text{[math]}$ ，底面 $\text{[math]}$ 为菱形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

(1) 若四棱锥 $\text{[math]}$ 的体积为 $\text{[math]}$ ，求 $\text{[math]}$ 的长；

(2) 求平面 $\text{[math]}$ 与平面 $\text{[math]}$ 所成钝二面角的正切值 $\text{[math]}$

解答题普通

3. 正四棱锥 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，其中 $\text{[math]}$ 为底面中心， $\text{[math]}$ 为 $\text{[math]}$ 上靠近 $\text{[math]}$ 的三等分点.

(1) 求四面体 $\text{[math]}$ 的体积；

(2) 是否存在侧棱 $\text{[math]}$ 上一点 $\text{[math]}$ ，使面 $\text{[math]}$ 与面 $\text{[math]}$ 所成角的正切值为 $\text{[math]}$ ？若存在，请描述点 $\text{[math]}$ 的位置；若不存在，请说明理由.

解答题普通