1.
有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90o后得到矩形AMEF(如图1),连接BD,MF,若BD=16cm,∠ADB=30o.
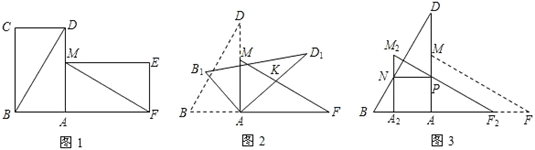
(1)
试探究线段BD 与线段MF的数量关系和位置关系,并说明理由;
(2)
把△BCD
与△MEF 剪去,将△ABD绕点A顺时针旋转得△AB1D1 , 边AD1交FM 于点K(如图2),设旋转角为β(0o<β<90o),当△AFK
为等腰三角形时,求β的度数;
(3)
若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.
【考点】
等腰三角形的性质;
矩形的性质;
平移的性质;
相似三角形的判定与性质;
旋转的性质;
