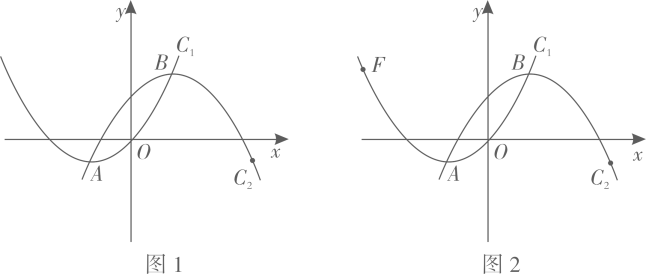
如图抛物线C1的顶点在抛物线C2上，抛物线C2的顶点也在抛物线C1上时.那么我们称抛物线C1与C2“互为关联”的抛物线.如图1，已知抛物线C1：y1= x2+x与C2：y2=ax2+x+c是“互为关联”的抛物线，点A，B分别是抛物线C1 ， C2的顶点，抛物线C2经过点D(6，-1).

1. 如图抛物线C₁的顶点在抛物线C₂上，抛物线C₂的顶点也在抛物线C₁上时.那么我们称抛物线C₁与C₂“互为关联”的抛物线.如图1，已知抛物线C₁：y₁= $\text{[math]}$ x²+x与C₂：y₂=ax²+x+c是“互为关联”的抛物线，点A，B分别是抛物线C₁ ， C₂的顶点，抛物线C₂经过点D(6，-1).

(1) 直接写出A，B的坐标和抛物线C₂的解析式：

(2) 抛物线C₂上是否存在点E，使得△ABE是直角三角形?如果存在.请求出点E的坐标；如果不存在，请说明理由：

(3) 如图2.点F(-6，3)在抛物线C₁上，点M、N分别是抛物线C₁ ， C₂上的动点，且点M，N的横坐标相同，记△AFM面积为S₁(当点M与点A，F重合时S₁=0)，△ABN的面积为S₂(当点N与点A，B重合时，S₂=0)，令S=S₁+S₂.观察图像.当y₁≤y₂时，写出x的取值范围.并求出在此范围内S的最大值.

【考点】

待定系数法求二次函数解析式; 二次函数与一次函数的综合应用; 二次函数-动态几何问题; 二次函数的实际应用-几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ，与y轴交于点C ，与x轴交于AB两点（A在B的左侧），连接AC ， BC ， $\text{[math]}$ .

(1) 求抛物线的表达式；

(2) 点P是射线CA上方抛物线上的一动点，过点P作 $\text{[math]}$ 轴，垂足为E ，交AC于点D.点M是线段DE上一动点， $\text{[math]}$ 轴，垂足为N ，点F为线段BC的中点，连接AM ， NF.当线段PD长度取得最大值时，求 $\text{[math]}$ 的最小值；

(3) 将该抛物线沿射线CA方向平移，使得新抛物线经过（2）中线段 $\text{[math]}$ 长度取得最大值时的点D ，且与直线AC相交于另一点K.点Q为新抛物线上的一个动点，当 $\text{[math]}$ 时，直接写出所有符合条件的点Q的坐标.

综合题困难

2. 如图，在平面直角坐标系中，抛物线y＝ax²+bx﹣4（a≠0）与x轴交于点A（﹣2，0）和点B（4，0），与y轴交于点C．

(1) 求抛物线的函数表达式；

(2) 线段DE位于第四象限，且在线段BC上移动，EF∥y轴交抛物线于点F，连接DF．若DE $\text{[math]}$ ，求△DEF的面积的最大值，及此时点E的坐标；

(3) 将该抛物线沿射线CB方向平移，使得新抛物线经过（2）中△DEF的面积取得最大值时对应的点E处，且与直线BC相交于另一点K．点P为新抛物线上的一个动点，当∠PEK和∠PKE中，其中一个角与∠ACB相等时，直接写出所有符合条件的点P的坐标，并写出其中一个点的求解过程．

综合题困难

3. 如图，在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点（点 $\text{[math]}$ 在 $\text{[math]}$ 轴上），与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，且 $\text{[math]}$ ．

(1) 求抛物线的解析式；

(2) 若 $\text{[math]}$ 为直线 $\text{[math]}$ 下方抛物线上的一个动点，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ．

①求线段 $\text{[math]}$ 的最大值；

②是否存在点 $\text{[math]}$ ，使得四边形 $\text{[math]}$ 为等腰梯形？若存在，请求出点 $\text{[math]}$ 的横坐标；若不存在，请说明理由．

综合题困难