1.
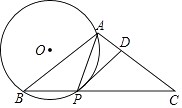
已知:如图,在△ABC中,AB=AC,点P是底边BC上一点且满足PA=PB,⊙O是△PAB的外接圆,过点P作PD∥AB交AC于点D.
(1)
求证:PD是⊙O的切线;
(2)
若BC=8,tan∠ABC=  ,求⊙O的半径.
,求⊙O的半径.
【考点】
勾股定理;
垂径定理;
切线的判定;
锐角三角函数的定义;


