1.
定义:在同一直线上有A,B,C三点,若点 C到A,B两点的距离呈2 倍关系,即AC=2BC 或BC=2AC,则称C是线段AB 的“倍距点”。

(1)
线段AB的中点(填“是”或者“不是”)该线段的“倍距点”。
(2)
已知AB=9,C 是线段AB 的“倍距点”,则AC=。
(3)
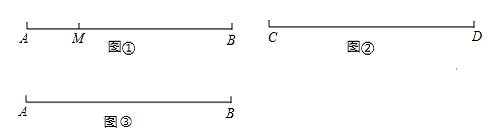
如图①,在数轴上,点A 表示的数为2,点 B 表示的数为 20,C 为线段 AB 的中点。
①现有一动点 P 从原点O 出发,以每秒2个单位长度的速度沿数轴向右匀速运动。设运动时间为t(s)(t>0),求当t为何值时,P为AC的“倍距点”。
②现有一长度为2的线段MN(如图②,点M起始位置在原点),从原点O出发,以每秒1个单位长度的速度沿数轴向右匀速运动。当N为MC 的“倍距点”时,请直接写出t的值。
【考点】
线段的中点;
数轴的点常规运动模型;
能力提升