1.
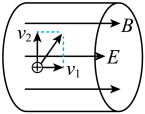
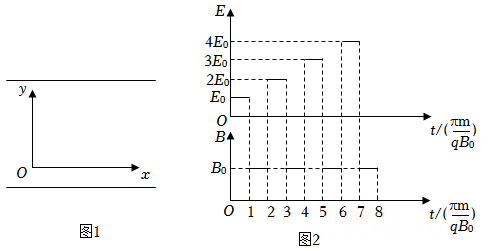
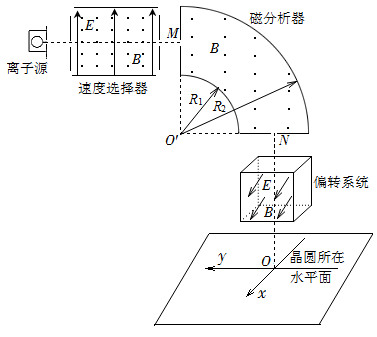
两水平放置的平行金属板M、N如图甲所示,板长L=0.4m,板间距d=0.4m。两金属板间加如图乙所示的电压UMN , 忽略电场的边缘效应。在金属板右侧有一矩形磁场区域abcd,ab=0.4m,ad=0.8m,O'为ad边的中点,磁场边界ad与金属板垂直,磁感应强度大小 , 方向垂直纸面向里。在极板左端有一粒子源,不断地向右沿着与两板等距的水平线OO'发射比荷
, 方向垂直纸面向里。在极板左端有一粒子源,不断地向右沿着与两板等距的水平线OO'发射比荷 、初速度大小
、初速度大小 的带负电粒子,忽略粒子受到的重力以及它们之间的相互作用,每个粒子在金属板间运动时电压可视为定值。零时刻射入平行板间的粒子恰好能经过b点,求:
的带负电粒子,忽略粒子受到的重力以及它们之间的相互作用,每个粒子在金属板间运动时电压可视为定值。零时刻射入平行板间的粒子恰好能经过b点,求:

(1)
粒子能射出金属板时的电压U的范围;
(2)
零时刻射入平行板间的粒子在平行板间和磁场中运动的总时间t;
(3)
粒子从bc边界离开磁场区域的宽度s。
【考点】
带电粒子在电场与磁场混合场中的运动;
能力提升
真题演练