1.
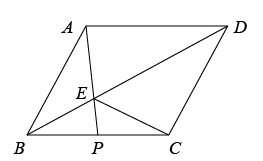
在正方形ABCD中,动点E , F在对角线AC上,连接DE , BF , 且DE∥BF .

(1)
如图1,若 ,
,  , 求CF的长度;
(2)
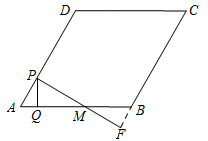
如图2,过点C作CG⊥AC , 且CE=CG , 连接AG , 分别交BF , BC于点H , K;若
, 求CF的长度;
(2)
如图2,过点C作CG⊥AC , 且CE=CG , 连接AG , 分别交BF , BC于点H , K;若 , 求证:
, 求证: ;
(3)
如图3,将线段DE绕着点D逆时针旋转60°,得到线段DE' , 连接CE' , BE';当线段DE' 取得最小值时,请直接写出
;
(3)
如图3,将线段DE绕着点D逆时针旋转60°,得到线段DE' , 连接CE' , BE';当线段DE' 取得最小值时,请直接写出 的值.
的值.
【考点】
四边形的综合;
四边形-动点问题;
能力提升
真题演练