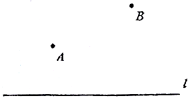
1.
已知:如图,由边长均为1个单位的小正方形组成的网格图中,点A、点 、点
、点 都在格点(正方形的顶点)上.
都在格点(正方形的顶点)上.

(1)
 的面积等于______个平方单位;
(2)
画出
的面积等于______个平方单位;
(2)
画出 关于直线
关于直线 的对称图形;
(3)
在直线
的对称图形;
(3)
在直线 上找一点
上找一点 , 使
, 使 的长最短.
的长最短.
【考点】
两点之间线段最短;
三角形的面积;
轴对称的性质;
作图﹣轴对称;