1.
综合探究
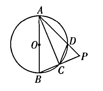
如题22图所示，AB为⊙O的直径，C，D为⊙O上的两点.且D为AC的中点，弦AC，BD相交于点E.
(1)
求证：△ADE∽△BD4；
(2)
若AB=8、∠AEB=122.5°，求
的长(结果用π表示)；
(3)
过点C作⊙O的切线，交AB的延长线于点F，若
求BF的长。
【考点】
圆周角定理;
切线的性质;
相似三角形的判定与性质;
解直角三角形;
弧长及其计算;
圆周角定理的推论;
