1.
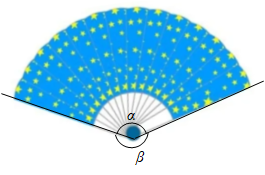
如图,直线AB,CD,相交于点O,∠MON=90°.∠BON比∠MOA多10°.求∠BON,∠MOA的度数若设∠BON=x°,∠MOA=y°.可列方程组为( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
二元一次方程组的应用-几何问题;