1.

(1)
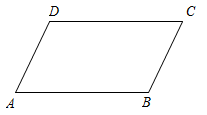
【教材改编】如图1,四边形ABCD是正方形,点G、E分别是边AB、BC的中点, , 且EF交正方形外角的平分线CF于点F . 求证:
, 且EF交正方形外角的平分线CF于点F . 求证: .
(2)
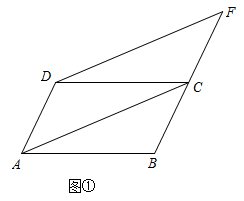
【类比探究】如图2,四边形ABCD是正方形,点E是BC边上的任意一点,
.
(2)
【类比探究】如图2,四边形ABCD是正方形,点E是BC边上的任意一点, , 且EP交正方形外角的平分线CP于点P . 求证:
, 且EP交正方形外角的平分线CP于点P . 求证: .
(3)
【知识迁移】在AB边上是否存在点M , 使得四边形DMEP是平行四边形?若存在,请在图3画出图形并给予证明:若不存在,请说明理由.
.
(3)
【知识迁移】在AB边上是否存在点M , 使得四边形DMEP是平行四边形?若存在,请在图3画出图形并给予证明:若不存在,请说明理由.
【考点】
平行四边形的判定与性质;
正方形的性质;
三角形全等的判定-SAS;
三角形全等的判定-ASA;