1.
[阅读理解]课外兴趣小组活动时,老师提出了如下问题:
如图1,在中,若
, 求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:如图2,延长AD到点E , 使
, 连结BE , 请根据小明的方法思考:
图1 图2
图2  图3
图3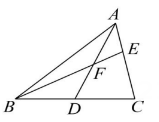
(1)
由已知和作图能得到 , 其理由是什么?
(2)
求AD的取值范围.
(3)
如图3,AD是
, 其理由是什么?
(2)
求AD的取值范围.
(3)
如图3,AD是 的中线,BE交AC于点F , 且
的中线,BE交AC于点F , 且 , 试说明
, 试说明 .
.
【考点】
三角形三边关系;
三角形全等及其性质;
三角形全等的判定-SAS;
能力提升


