1.
如图1,将两块直角三角板(一块含有 、
、 角,另一块含
角,另一块含 角)摆放在直线
角)摆放在直线 上,三角板
上,三角板 绕点
绕点 以每秒
以每秒 的速度逆时针旋转.当
的速度逆时针旋转.当 第一次与射线
第一次与射线 重合时三角板
重合时三角板 停止转动,设旋转时间为
停止转动,设旋转时间为 秒.
秒.
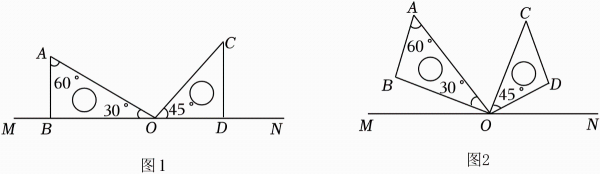
(1)
当 时,求
时,求 和
和 的度数;
(2)
如图2,若两块三角板同时旋转,三角板
的度数;
(2)
如图2,若两块三角板同时旋转,三角板 以每秒
以每秒 的速度绕点
的速度绕点 顺时针旋转,当
顺时针旋转,当 第一次与射线
第一次与射线 重合时三角板
重合时三角板 立即停止转动.
立即停止转动.
①用含的代数式表示射线
和射线
重合前
和
的度数;
②整个旋转过程中,当满足时,求出相应的
的值.
【考点】
旋转的性质;
一元一次方程的实际应用-几何问题;
能力提升

