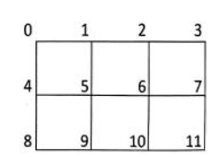
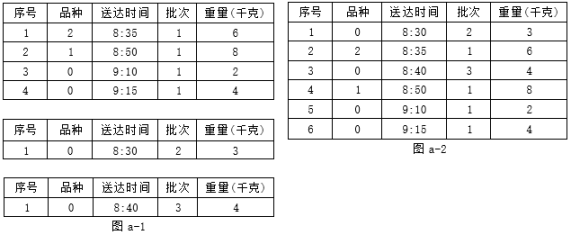
最短路径问题。以 m*n 个边长为 1 的正方形组成的矩形，各顶点按行优先从 0 开始编号，如图 a 所示为 3*2 的矩形及顶点编号。从顶点 x（起点）经由各正方形的边移动到顶点 y（终点）有多种移动路径，编程求解所有的最短路径。图 a 图 b

0 返回首页

1. 最短路径问题。以 m*n 个边长为 1 的正方形组成的矩形，各顶点按行优先从 0 开始编号，如图 a 所示为 3*2 的矩形及顶点编号。从顶点 x（起点）经由各正方形的边移动到顶点 y（终点）有多种移动路径，编程求解所有的最短路径。

图 a

图 b

(1) 分析问题，将矩形转换为计算机可处理的数据。可采用列表存储矩形中各顶点的相邻关系，如图 b所示。

编写函数init，根据横向和纵向的正方形数量，返回所有顶点及其所有的相邻顶点数据。完善程序，在划线处填入合适的代码。

def init(m,n):

tot=(m+1)*(n+1) #顶点总数

lst=[[] for i in range(tot)]

for i in range(tot):

if i>m:

lst[i].append(i-m- 1)

if i<(m+1)*n:

lst[i].append(i+m+1)

if i%(m+1) != 0:

lst[i].append(i- 1)

if i%(m+1) != m:

return lst

(2) 分析问题，查找所有从起点到终点的最短路径。例如：查找从起点1到终点10的所有最短路径，可先查找终点10的所有相邻顶点（6,9,11），然后再逐个查找顶点6、9、11的相邻顶点，直到查找到起点1，获得所有最短路径，如图c所示，共有3条长度为3的最短路径，分别为1→2→6→10,1→5→6→10,1→5→9→10。若从起点4到终点11，共有（填数字）条最短路径。

图 c

(3) 分析问题，存储查询到的路径。可采用链表结构保存路径数据，例如：查找从起点1到终点10的所有最短路径，首先将终点10的数据[10,0,-1]保存在path[0]中，然后将其相邻顶点6、9、11的数据保存到path中，path[i][0]保存顶点的编号，path[i][1]保存当前顶点到终点的距离，path[i][2]保存下一顶点在path中的位置，其值为-1表示当前顶点为终点。

编写函数print_path，输出所有的最短路径。完善程序，在划线处填入合适的代码。

def print_path(x,path,length): #为起点编号，length为Path中有效元素个数。

cnt=0

for i in range(length):

if path[i][0] == x:

cnt+= 1

s="最短路径"+str(cnt)+":"

v=path[i]

while :

s=s+str(v[0])+","

v=path[v[2]]

s=s+str(v[0])+" 。"

print(s)

(4) 实现上述功能的 Python程序如下，运行结果如图 d 所示。请在划线处填入合适的代码。

m=3 #横向正方形数量

n=2 #纵向正方形数量

mtx=init(m,n)

x=int(input("请输入起点:"))

y=int(input("请输入终点:"))

path=[[] for i in range(30)]

passed=[False]*len(mtx) #保存顶点是否已途经

dis=0

head=0

tail=0

path[tail]=[y,0,- 1]

tail+= 1

passed[y]=True

while not found:

dis+= 1

pass_dis=[False]*len(mtx)

tmp=tail

for i in range(head,tail):

v=path[i]

for d in mtx[v[0]]:

if not passed[d]:

path[tail]=

tail+= 1

pass_dis[d]=True

if d == x:

found=True

head=tmp

for i in range(len(mtx)): #标记已途经的顶点

if :

passed[i]=True

#输出结果

print_path(x,path,tail)

【考点】

过程与自定义函数; 循环结构语句及程序实现; 基本数据结构;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 某工厂将送达的各批次物品按品种打包。小李将各批次物品信息按送达时间顺序合并，得到如图 a-2 所示数据 data。同一个包裹只能装入同一品种任意批次的物品，当某一个品种物品 A 送达使得已送达的该品种物品总重量超过 m 时，则将在该物品之前送达的物品按重量由大到小依次装入包裹,其余重量不足 m 的品种，按各品种依次装入包裹。编写程序，读取物品合并更新后的信息，按送达时间顺序打包，输出各包裹中的物品序号，运行结果如图 b 所示。

请回答下列问题：

(1) 送达物品信息合并后如图 a-2 所示，若包裹装入物品重量不能超过 8 千克，则首先打包完成的包裹中装入品种为 0，各物品的序号依次是。

(2) 定义 data_sort(lst)函数。先将数据（如图 a-1 中所示）合并得到 lst 列表（如图 a-1 中所示），函数 data_sort(lst)的功能是对 lst 列表按送达时间升序排列，并对序号进行更新。

def data_sort(lst):

for i in range(n- 1):

for j in range(n- 1,i,- 1):

if lst [j][2]< lst [j- 1][2]:

lst [j], lst [j- 1]= lst [j- 1], lst [j]

lst[i][0]=i+1

return lst

执行上述代码后， (填写：能/不能）正确得到如图 a-2 中的数据。

(3) 实现上述功能的部分Python程序如下，请在划线处填入合适的代码。

def pack(k): #对品种 k已送达待打包的物品按重量由大到小输出

#部分代码略

p=b[k][1]

num+= 1

print("第"+str(num)+"个包裹中品种为"+str(k)+" ，各物品的序号依次是：",end=" ")

while p!=- 1:

print(data[p][0],end=",")

p=x[p]

print()

'''

合并后排序得到 n 件物品的数据存储在数组 data 中并输出，包裹最大承受最大重量为 m 千克。物品品种的数量是 sn ，代码略

'''

b=[[0,- 1] for i in range(sn)]

x=[- 1 for i in range(n)]

num=0

for i in range(n):

k=data[i][1]

if b[k][0]+data[i][4]>m :

pack(k)

b[k]=[0,- 1]

if p==- 1:

b[k][1]=i

else:

if data[i][4]>data[p][4]:

b[k][1]=i

else:

q=- 1

while :

q=p

p=x[p]

x[q]=i

x[i]=p

b[k][0]+=data[i][4]

#重量不足 m 的品种，按各品种依次装入包裹

for i in range(sn):

if b[i][1]!=- 1:

pack(i)

综合题困难

2. 某医院的看病流程为：患者通过网上、自助设备或人工窗口成功挂号后，到门诊的签到处签到，签到成功后即可排队等待叫号就诊。简化的排队规则如下：

①当天08:00之前完成签到的患者，按照挂号顺序从小到大排队就诊；

②08:00之后签到的患者，按照挂号的序号从小到大的次序插入候诊队伍中；

③队伍中前3名患者(包括正在就诊患者)视为已进入待诊状态，插队的患者只能插到这3 名待诊患者后的队伍中。

假设医生从08:00开始叫号就诊，对每位患者的诊断时间均为3分钟，忽略相邻患者就诊的时间间隔。编写程序实现以下功能：若有患者签到，则根据规则更新候诊队伍；医生每完成一名患者的诊断，电子屏幕上按顺序显示待诊的患者姓名和每个患者预计就诊的时间。

(1) 若当前已签到患者信息如下表所示：

姓名	挂号序号	签到时间
A	3	07:47:03
B	1	07:51:12
C	6	07:55:32
D	4	07:57:10
E	8	07:59:52
F	2	08:02:07

则患者 F的预计就诊时间为 (格式如08:07:20)。

(2) 08:00:00之前签到的患者原始数据存在列表1st 中，每位患者信息包括姓名、挂号序号、签到时间，以下函数将列表中的数据按挂号序号从小到大排序，并构建候诊队伍。

def init(lst): #构建8点前签到的候诊队伍

i=0;n=len(lst)

while i<n-1:

k=i;i=n-1

for j in range(n-1,k,-1):

if lst[i][1]<lst[j-1][1]:

lst[j],Ist[j-1]=Ist[j-1],Ist[j]

____▲____

for i in range(n):

lst[i][2]=180*i

lst[i].append(i+1)

lst[n-1][3]=-1

#修改时间格式，每位患者诊断时间为3分钟

#尾结点指针域处理，如[’E’,8,720,-1]

程序划线处的代码是 (单选，填字母)

A. i=i+1 B. i=j+1 C. i=k-1 D. i=j

(3) 每当一位患者就诊结束，更新队伍并按就诊顺序输出待诊的患者姓名和每个患者预计就诊的时间。请补充程序划线处。

def gs(t):# 时间格式转换，将时间戳127转成“08:02:07”形式

t=t+8*60*60

h=t//3600

s=t%60

time='%02d'%h+:'+'%02d%m+:+'%02d'%s

return time

def mov(lst,head):

#更新队伍并输出，代码略

return head

(4) 若有患者签到，则更新候诊队伍。请补充程序划线处。

def te(time): #时间格式转换，将“08:02:07”转换成以秒为单位的时间戳127

t=int(time[0:2])*60*60+int(time[3:5])*60+int(time[6:])

t=t-8*60*60 #8 点开始叫号看诊

return t

def insnew(lst,head,data); #将新签到的患者插入候诊队伍中，并更新每个患者预计就诊的时间

data[2]=tc(data[2])

data.append(-1)

p=head;q=p;k=0

if head=-1:# 无人排队

lst.append(data)

else:

while q!=-1 and():

k=k+1

p=q

q=lst[q][3]

data[2]=lst[p][2]+180

data[3]=q

lst.append(data)

lst[p][3]=len(lst)-]

p=len(lst)-1

while q!=-1:

lst[q][2]=1st[p][2]+180

p=q

q=lst[q][3]

return head

综合题困难

3. 魔术师预先将一副牌中的 13张黑桃(A为1，J为11，Q为12， K为13)排好后叠在一起，牌面朝下。他将最上面的那张牌翻过来，正好是黑桃A。将黑桃A放在桌子上，然后按顺序从上到下数手上的余牌：第二次数1、2，将数到的第一张牌放在这叠牌的下面，将第二张牌翻过来，正好是黑桃2，将它放在桌子上；第三次数1、2、3，将前面两张依次放在这叠牌的下面，再翻第三张牌，正好是黑桃3，放在桌子上。这样依次进行，将13张牌全翻出来，最后桌子上牌的顺序是A、2、3、……、K。问魔术师手中的牌原始顺序是怎样的？

小王和小李对问题进行了分析与算法设计，写了Python函数way()正确解答了问题，请回答下列问题。

(1) 原来牌的顺序中，黑桃3放在自上向下第(填阿拉伯数字)个位置。

(2) 请在划线处填入合适的代码。

def way() ：

a=[i for i in range(1， 14)]

b=[0]*13#0代表牌面未定

head=0；tail=0

for i in range(1， 14)：

cnt=1

while cnt < i：

a[tai1]= ①

head = (head+1)%13

tail = (tail+1)%13

②

③

head = (head+1)%13

return b

print (way())

①②③

综合题困难