1.
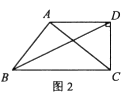
在平面内，先将一个多边形以自身的一个顶点为位似中心放大或缩小，再将所得多边形沿过该点的直线翻折，我们称这种变换为自位似轴对称变换，变换前后的图形成自位似轴对称．
例如：如图①，先将以点
为位似中心缩小，得到
， 再将
沿过点
的直线
翻折，得到
， 则
与
成自位似轴对称．
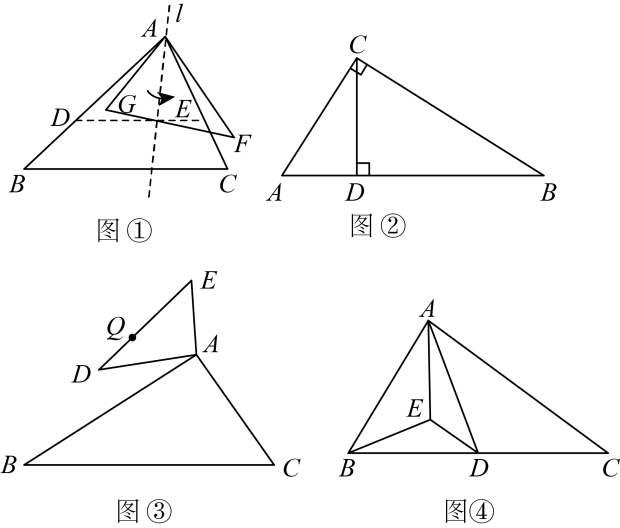
(1)
如图②，在
中，
， 
， 
， 垂足为
， 下列3对三角形：①与
；②
与
；③
与
． 其中成自位似轴对称的是（填写所有符合条件的序号）；
(2)
如图③，已知经过自位似轴对称变换得到
， 
是
上一点，用直尺和圆规作点
， 使与是该变换前后的对应点（保留作图痕迹，写出必要的文字说明）；
(3)
如图④，在中，是
的中点，
是内一点，
， 
， 连接 ， 求证：
．
【考点】
轴对称的性质;
相似三角形的判定与性质;
作图﹣相似变换;
