1.
问题背景:

(1)
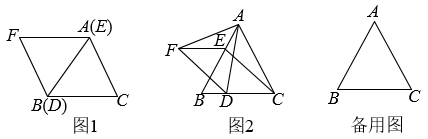
如图1,在四边形 中,
中, ,
,  ,
,  ,
,  ,
,  分别是
分别是 ,
,  上的点,且
上的点,且 , 探究图中线段
, 探究图中线段 、
、 、
、 之间的数量关系,嘉琪同学探究此问题的方法是:延长
之间的数量关系,嘉琪同学探究此问题的方法是:延长 到点
到点 , 使
, 使 , 连接
, 连接 , 先证明
, 先证明 , 再证明
, 再证明 , 可得出结论,他的结论应是.
(2)
探索延伸:①如图2,若在四边形
, 可得出结论,他的结论应是.
(2)
探索延伸:①如图2,若在四边形 中,
中, ,
,  ,
,  、
、 分别是
分别是 ,
,  上的点,且
上的点,且 , 上述结论是否仍然成立,并说明理由.
, 上述结论是否仍然成立,并说明理由.
②如图2,若五边形的面积为30,
,
, 直接写出
点到
的距离.
【考点】
三角形全等的判定-SAS;
三角形的综合;
能力提升
真题演练