如图，点O是等边△ABC内一点，∠AOB=100°，∠BOC=α．以OC为边作等边△OCD，连接AD．

1. 如图，点O是等边△ABC内一点，∠AOB=100°，∠BOC=α．以OC为边作等边△OCD，连接AD．

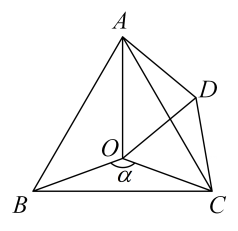
(1) 求证：△BOC≌△ADC；

(2) 当a=150°时，试判断△AOD的形状，并说明理由；

(3) 探究：当α为多少度时，△AOD是等腰三角形？

【考点】

等腰三角形的判定; 等边三角形的性质; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，△ABC是等边三角形，BD是AC边上的高，延长BC至E，使DB=DE.

(1) 求∠BDE的度数；

(2) 求证：△CED为等腰三角形.

综合题普通

2. 如图， $\text{[math]}$ 是等边三角形， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点，连接 $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ ；

(2) 在线段 $\text{[math]}$ 的延长线上取点 $\text{[math]}$ ， $\text{[math]}$ ，使 $\text{[math]}$ ，直线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ．

①求证： $\text{[math]}$ ；

②请判断 $\text{[math]}$ 的形状，并说明理由．

综合题困难

3. 已知：线段 $\text{[math]}$ 及过点A的直线l．如果线段 $\text{[math]}$ 与线段 $\text{[math]}$ 关于直线l对称，连接 $\text{[math]}$ 交直线l于点D，以 $\text{[math]}$ 为边作等边 $\text{[math]}$ ，使得点E在 $\text{[math]}$ 的下方，作射线 $\text{[math]}$ 交直线l于点F，连结 $\text{[math]}$ ．

(1) 根据题意补全图形；

(2) 如果 $\text{[math]}$ $\text{[math]}$

① $\text{[math]}$ ▲ ；（用含有 $\text{[math]}$ 代数式表示）

②用等式表示线段 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并证明．

综合题普通