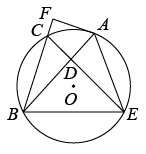
如图，已知AB是⊙O的弦，点C是弧AB中点，D是弦AB上一动点，且不与A、B重合，CD的延长线交⊙O于E，连接AE、BE，过点A作，垂足F，.

1. 如图，已知AB是⊙O的弦，点C是弧AB中点，D是弦AB上一动点，且不与A、B重合，CD的延长线交⊙O于E，连接AE、BE，过点A作 $\text{[math]}$ ，垂足F， $\text{[math]}$ .

(1) 求证：AF是⊙O的切线；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，则DE的长是多少？

(3) 当点D在弦AB上运动时， $\text{[math]}$ 的值是否发生变化？如果变化，写出其变化范围；如果不变，求出其值.

【考点】

等边三角形的判定与性质; 圆周角定理; 切线的判定; 相似三角形的判定与性质; 锐角三角函数的定义;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知，如图，△ABC的顶点A，C在⊙O上，⊙O与AB相交于点D，连接CD，∠A＝30°．

(1) 若⊙O半径为3，求弦CD的长；

(2) 若∠ACB＋∠ADC＝180°，求证：BC是⊙O的切线．

综合题普通

2. 如图，已知 $\text{[math]}$ 是 $\text{[math]}$ 的外接圆，AB是 $\text{[math]}$ 的直径，P是AB的延长线上的一点，弦CE交AB于点D， $\text{[math]}$ ； $\text{[math]}$ ．

(1) 求证：PC是 $\text{[math]}$ 的切线；

(2) 若 $\text{[math]}$ ，求弦EC所对圆周角的度数．

综合题普通

3. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为直径的 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，垂足为 $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线．

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

综合题普通