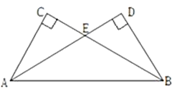
1.
在正方形  中,
中,  为对角线
为对角线  上任意一点(不与
上任意一点(不与  重合)连接
重合)连接 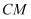 ,过点M作
,过点M作  交
交  (或
(或  的延长线)于点N,连接
的延长线)于点N,连接  .
.

感知:如图①,当M为 中点时,容易证
(不用证明);
(1)
探究:如图②,点M为对角线  上任意一点(不与
上任意一点(不与  重合)请探究
重合)请探究  与
与 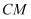 的数量关系,并证明你的结论.
(2)
应用:
的数量关系,并证明你的结论.
(2)
应用:
直接写出 的面积S的取值范围;
(3)
若
的面积S的取值范围;
(3)
若  ,则
,则  与
与  的数量关系是.
的数量关系是.
直接写出
【考点】
全等三角形的判定与性质;
等腰三角形的判定与性质;
正方形的判定与性质;