0 返回首页
1. 如图所示，已知直角三角形纸板ABC，直角边AB=4 cm，BC=8 cm.

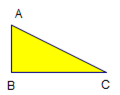
(1) 将直角三角形纸板ABC绕三角形的边所在的直线旋转一周，能得到种不同的几何体；
(2) 分别计算绕三角形直角边所在的直线旋转一周，得到几何体的体积.（ 取3）
【考点】
点、线、面、体及之间的联系;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1.

观察下图并按要求回答问题。


(1) 如图，（1）、（2）、（3）、（4）为四个平面图形，请数一数：每个平面图形各有多少个顶点？多少条边？它们分别围成了多少个区域？请你将结果填入下表．

图形

顶点数

边数

区域数

（1）

4

6

3

（2）

 

 

（3）

 

 

（4）

 

 
(2) 观察上表，推断一个平面图形的顶点数，边数，区域数之间有什么关系？
综合题 普通
2. 一个直角三角尺的两条直角边长是6和8，它的斜边长是10，将这个三角尺绕着它的一边所在的直线旋转一周．（温馨提示：①结果用π表示；②你可能用到其中的一个公式，V圆柱=πr2h，V球体=πR3 ， V圆锥=πr2h）．

(1) 如果绕着它的斜边所在的直线旋转一周形成的几何体是两个圆锥形成的几何体．
(2) 如果绕着它的直角边6所在的直线旋转一周形成的几何体的体积是多少？
(3) 如果绕着斜边10所在的直线旋转一周形成的几何体的体积与绕着直角边8所在的直线旋转一周形成的几何体的体积哪个大？
综合题 普通