1.
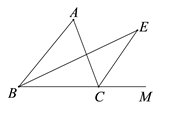
如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中,正确的有( )

A.
1个
B.
2个
C.
3个
D.
4个
【考点】
三角形的外角性质;
角平分线的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练