1.
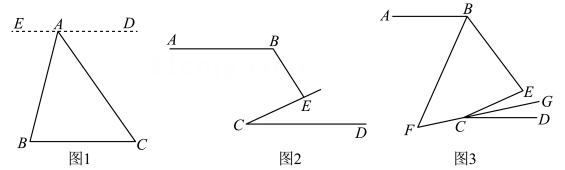
(1)
阅读并补全上述推理过程.
(2)
如图2所示,已知 交于点E,∠BEC=85°,在图2的情况下求∠B-∠C的度数.
(3)
如图3,已知
交于点E,∠BEC=85°,在图2的情况下求∠B-∠C的度数.
(3)
如图3,已知 交点E,BF、CG分别平分
交点E,BF、CG分别平分 , 直线BF与直线CG交于点
, 直线BF与直线CG交于点 , 若
, 若 , 则∠BEC=.
, 则∠BEC=.
如图1,已知点A是BC外一点,连接AB,AC.求的度数.
解:过点作
,
,
,
又.
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将“凑”在一起,得出角之间的关系,使问题得以解决.
【考点】
平行公理及推论;
平行线的性质;
角平分线的概念;


